The task of deconvolution of spot-based spatial transcriptomics (ST) data consists in finding the cellular composition in spots of ST assays. Indeed, by design each spot consists of several individual cells. Our lab developed destVI as a tool to study cell type composition of spots (1). In the case where one expects within cell type variation (i.e., activation states), DestVI was designed to infer the activation state of individual cell types in each spot and therefore gives additional resolution of cell composition over competing algorithms. In our own benchmarking of destVI, we found comparable performance in prediction of cell type proportions to other state of the art algorithms like Cell2Location (2). A recent benchmarking study compared the performance of several gene imputation as well as deconvolution methods. Given the ever increasing number of deconvolution methods, the effort to benchmark those tools on a variety of simulated data is timely (3). In two of the benchmarking cases, DestVI had the worst performance. Along with the recent acceptance of the manuscript, we published several fixes to the codebase in scvi-tools v0.16.0, repeated those experiments and analyzed the reasons for failure of spot deconvolution in the given experiments. Briefly, we show that the poor performance was due to the mini-batch size used during optimization, and resolving this help recovering competitive accuracy. Additionally, we provide the user with a heuristic for future use.

More specifically, variational autoencoders are a specific type of neural networks (NN) that, like most NN, are trained by iteratively presenting the network mini-batches of data, that is a small fraction of the whole dataset. The mini-batch size refers to number of distinct samples used for updating the parameters of the neural networks during one training step.

Methodology#

Models#

The DestVI model (1) uses a first training phase on a reference single cell dataset to learn a cell-type specific latent space. Then, it learns a second model using as input the spot data, and encoding them in the reference latent space. Finally, the model learns cell-type proportions for each spot. In this blog post, we only address the cell-type proportion estimate as was done in the original benchmarking study (3). We haven't checked the activation state of those cells as the simulation was designed in a way where the mean activation state of each cell-type in each spot is not known and ground-truth therefore is missing. For all experiments here, we kept the parameters for the CondSCVI model on which the single-cell data is learned constant and highlight every parameter we changed in the respective run. The only two parameters that we highlight here are the amortization scheme, where destVI allows a neural network for amortization of cell-type proportions and activation state or models them as free parameters, and the mini-batch size used for training.

The selection of genes for destVI used in the original benchmarking study is a point we wanted to mention here. The authors first took the intersection of the genes in spatial assay and single cell assay (882 genes overlapping for STARmap dataset) and then took the 2000 highly variable genes. This second step was without effect (2000 is higher than 882). Nevertheless, in case a FISH based experiments was designed specifically for an organ and all genes were carefully selected, we generally would recommend against additional filtering for over-dispersed genes in a single cell reference but train the model directly on the overlap of spatial and single cell genes skipping the step of highly variable genes.

We compare destVI throughout this blog post with the benchmark version of Cell2Location. Our purpose is not to prove that we outperform other existing methods but to analyze why destVI showed poor performance in the benchmarking study. Cell2Location showed overall good performance in the benchmarking study and is implemented using the scvi-tools framework but relies on a marker gene related approach instead of an unbiased deconvolution approach.

Hyperparameter selection#

Most experiments before the destVI publication, as well as the benchmarking study were performed using cell-type activation state amortization only (called latent amortization hereafter) and treat the cell-type proportions as a free parameter. However, in the recent version of the code we generally recommend to use the amortized version of both (called both amortization hereafter). In this blog post, we checked performance in all experiments here for both amortization schemes. The size of the training mini-batch size varied as {4, 8, 16, 32, 64, 128, 256, 512, 1024}. For comparison with the benchmarking study we left out batch sizes 256 or higher because the number of spots was 189. For our comparison, in a large scale dataset we left out batch_sizes 16 and lower because the training time drastically increases when using small batch sizes on large datasets.

Results#

Datasets#

We reused the STARmap dataset from the original publication (mouse brain cortex). The single-cell reference contains 14,249 cells by 34,041 genes. It contains data from several mouse lines, both sexes and from various time points that were sorted by flow cytometry and sequentially sequenced. The STARmap dataset contains 1,523 cells by 981 genes. The simulation is to sum all counts over a window size of 750 pixels. This gives a pseudo-spot count matrix with 189 spots and 1-17 cells per spot. For further reference, we refer to the original publication (3). We subset this dataset to 57 spots to see how destVI performs in the case of even lower number of spots by subsetting this data to the first three column as diversity of cell-types is mainly along the cortical axis and subsetting to columns keeps the complexity of the dataset similar.

For a regime with more spots, we decided to keep the organ of interest (mouse brain) and use a dataset with a much higher number of cell captured. We reproduced for this matter the analysis provided by Vizgen using MERFISH technology, which provides a walk-through tutorial on Google Colab.

Figure 1: Overview of MERFISH brain dataset from (https://colab.research.google.com/drive/1OxJRO19cPsDW0JGAh4tLJjgOl7EMxQbP?usp=sharing&__hstc=30510752.37206d737856c71bb0a5d1c8f6764b63.1652985789816.1653807477271.1653882474080.8&__hssc=30510752.1.1653882474080&__hsfp=455698764&hsCtaTracking=070f4af1-2595-44c8-9779-4da89d538482%7Cf4313de5-25c4-4677-9fd6-82cf71d4fdc4).

This analysis yields a single-cell reference dataset with 160,796 cells by 27,998 genes and a spatial dataset with 83,546 cells by 483 genes. The simulation here is again to sum all counts of cells with a center over a window of 40 µm. We choose the size of this window to have an equal number of cells per pseudo-spot compared to the STARmap dataset. This gives a pseudo-spot count matrix with 27395 spots and 1-16 cells per spot.

Results on STARmap dataset#

First, we verified that by using the updated version of the code in scvi-tools v0.16.0, we get similar results to the benchmarking study. In agreement with the original benchmarking study, the layer structure of neurons in different cortical layers wasn't visible.

Then, we ran different amortization variants of DestVI. Modeling cell-type proportions as a free parameter leads to no visible structure at all (as was run by the study). When using amortized cell-type proportions, which uses a neural network to estimate cell-type proportions, destVI predicted astrocytes correctly, while it wasn't capable of differentiating different excitatory neurons but were classifying all neurons as a single mixture.

By changing the batch-size, we noticed that decreasing the training mini-batch size drastically improves the performance of both algorithms. Notably, the model with a mini-batch size of 32 and both parameters amortized performs badly. We see good deconvolution of the different neuronal layers with a batch size of 8, 12 and 16. Additionally, for these batch size there was no qualitative difference between both amortization and latent amortization.

When comparing the results of destVI with Cell2Location it becomes clear that Cell2Location outperforms destVI for cell-types like Pvalp or Smc cells while both algorithms fail on microglia. The reason for better performance of Cell2Location is most likely low number of those cell-types in the spatial dataset and therefore low percentage in the respective spot. The bad performance for microglia might be based on the selection of FISH probes giving a low coverage of myeloid cell heterogeneity.

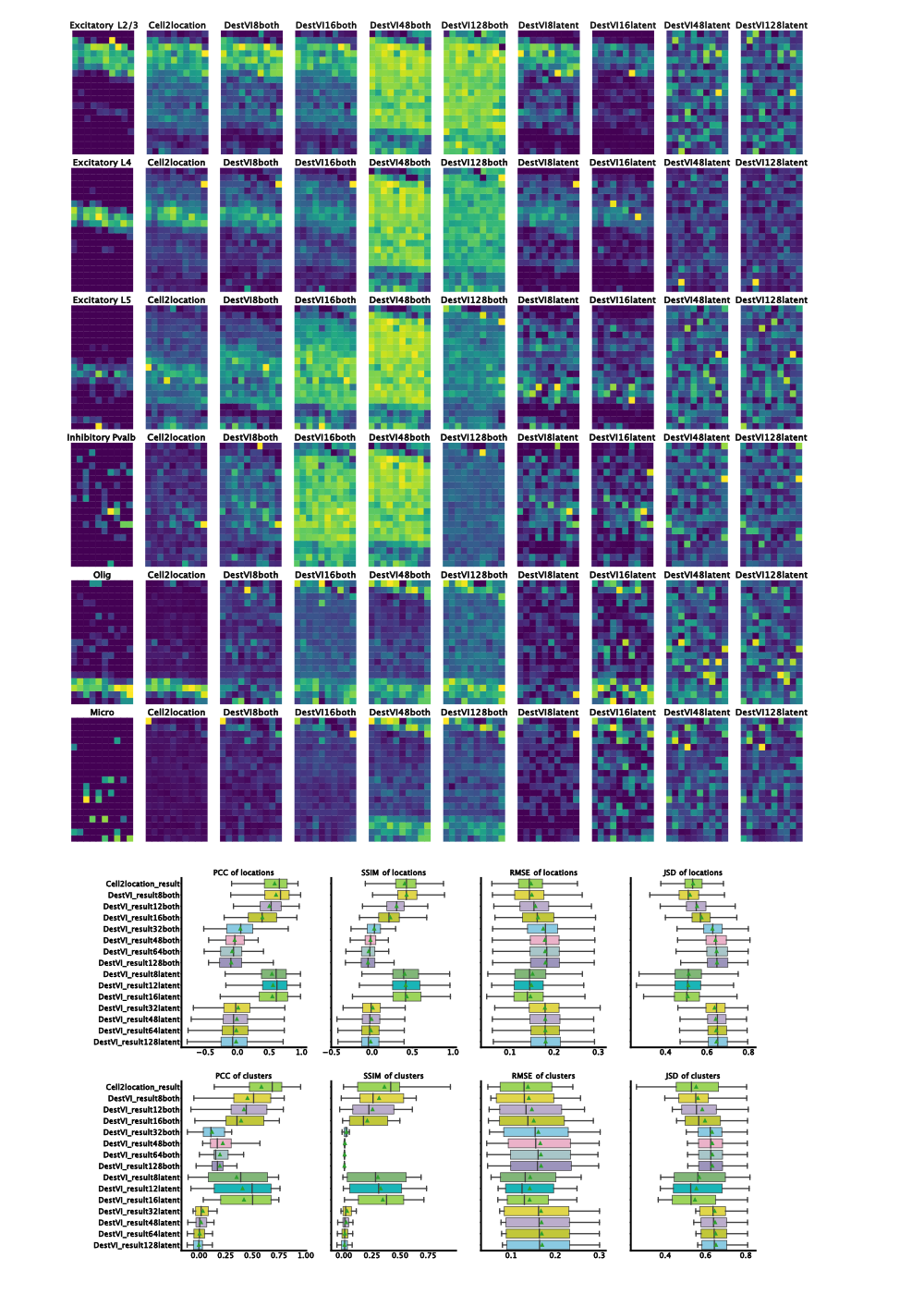
Figure 2: Results on benchmarking dataset. Left-to-right ground truth, Cell2Location, DestVI with both amortization and batch-size 8, 16, 48, 128 and DestVI with latent amortization with same batch size. Increase in matching proportions for destVI with decreasing mini-batch size. Cell2Location outperforms destVI for Oligodendrocytes. Quantitative measurues (PCC=Pearson Correlation Coefficient, SSIM=Structural Similarity, RMSE=Root Mean Squared Error, JSD=Jensen-Shannon-Divergence) show on par performance for destVI with a mini-batch size below 16.

When checking quantitative results, we find on par performance of destVI and Cell2Location in Pearson Correlation Coefficient based on spots while when checking for correlation across cell-types Cell2Location outperforms destVI. The reason for this improved performance are as described above lowly abundant cell-types.

As demonstrated here, by reducing the size of the training mini-batch destVI yields overall similar performance to Cell2Location for cell-type deconvolution. We asked next whether this is also the case when even further reducing the number of spots. For this study, as described above we subset the number of pseudo-spots and retrained Cell2Location and destVI. Overall, we find better agreement with both amortization for different sizes of training batch size. Oligodendrocytes and Astrocytes are correctly predicted in all version with both amortization. Only the models with a batch size of 4 differentiate between the different layers of excitatory neurons. Of note, latent amortization outperforms both amortization here for a mini-batch size of 4. It might be an effect of small training size, so that the amortization network can not be trained well. We generally wouldn't recommend to use spatial deconvolution techniques for such low number of spots. Given the higher stability over a various number of mini-batch sizes, we prefer to recommend using both amortization scheme. In cases with very few examples and known ground-truth we advise training both models and comparing the results.

Figure 3: Results on subset of benchmarking dataset. Subset on first three columns in original dataset. Displayed are only neuron layers as structure in other celltypes is hardly detected with only three columns. For ground-truth, we display all columns to allow easier comparison. Left-to-right ground truth, Cell2Location, DestVI with both amortization and batch-size 4, 8, 12, 16, 32 and DestVI with latent amortization with same batch size. On par performance with mini-batch size 4 and latent amortization is visible with slightly reduced performance in both amortization.

Results on MERFISH dataset#

To check the effect of training mini-batch size on the performance of large datasets, we simulated a second pseudospot matrix. The training time increases drastically with reducing the mini-batch size as the GPU is used less efficiently. We therefore restricted to models with a mini-batch size above 32 (trained more than 3 hours on a Nvidia RTX 3090). We therefore think that the mini-batch size should be 128, in which case we haven't seen major speed improvement (most likely depends on the GPU architecture).

Overall, for all combinations of parameters we see improved performance of destVI over standard Cell2Location. This is especially visible in Di- and mesencephalon excitatory neurons and Telencephalon inhibitory inter-neurons where Cell2Location doesn't uncover the tissue distribution of this cell-type. We see here no correlation to small size of those cell-types, and the reason for this reduced performance is not clear. As we haven't set out a benchmarking study here, but to study the performance of destVI, we haven't changed the hyper-parameters for Cell2Location to increase performance.

Overall we see that performance is stable up to a batch size of 256 with decreasing performance for both amortization and batch size 512 and 1,024, while performance of latent amortization is stable with increasing batch size. We postulate that mini-batch training of the cell-type amortization network is essential for performance. As above we have seen speed improvement by using a bigger batch size, we asked whether bigger batch sizes are good in performance, when we train them for more epochs. Indeed increasing the number of epochs for mini-batch size 512 lead to on par performance using 5,000 instead of the default 2,500 training epochs, while performance of mini-batch size 1,024 was still inferior when checking with 10,000 training epochs.

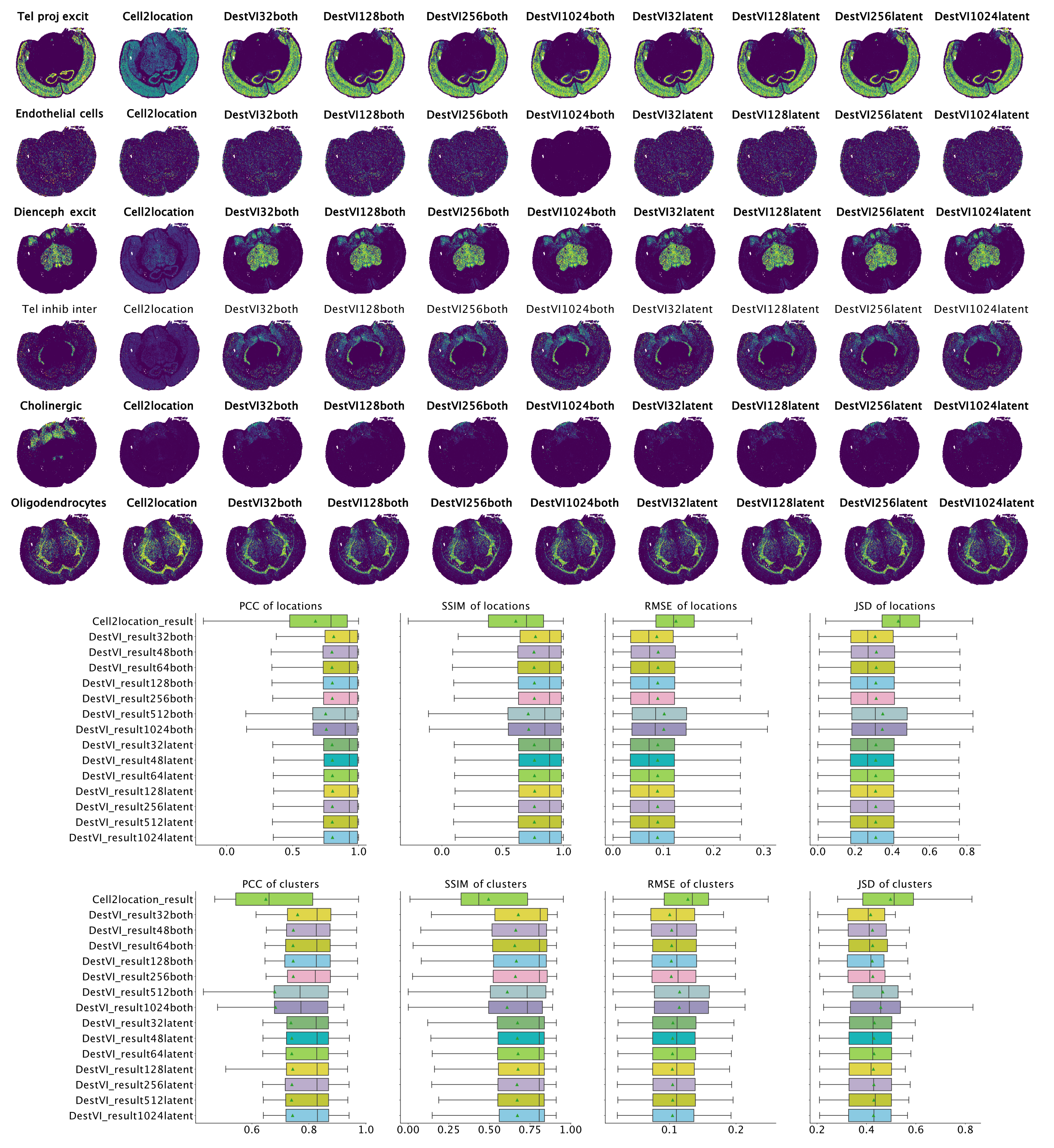
Figure 4: Results on MERFISH brain dataset. Left-to-right ground truth, Cell2Location, DestVI with both amortization and batch-size 32, 128, 256, 1,024 and DestVI with latent amortization with same batch size. Cell type proportion estimates are improved over Cell2Location in all destVI models. There is a decrease in performance for models with batch_size 1,024 for endothelial cells, that are low abundant in every spot.

Conclusion#

In the analysis of destVI from the main paper, we had limited our benchmarking to standard spot based assays, in which both spatial and single cell data sets are based on whole transcriptome sequencing and especially contain more than 1,000 spots. We found that DestVI performance from the newly published benchmarking study was mediocre because the number of spots was close to the training mini-batch size and therefore the underlying composition of the spots was not learned adequately. We verified this by proving that by decreasing training mini-batch size, destVI can yield on par performance to other methods for cell type deconvolution.

DestVI yields not only cell-type proportion estimates but also cell-type activation estimates, the benchmarking study was designed to only study cell-type proportion estimates and we kept the same design here. Generally, we think the additional output of cell-type activation is a major benefit of DestVI over competing algorithms. We nevertheless thank the authors of the original benchmarking study to discover deficiencies of destVI with small number of spots.

Practical recommendations#

We demonstrated that destVI also yields those results with a subset of the original dataset with just 57 spots. We also checked 19 spots here and destVI and Cell2Location weren't discovering the different layers of cortical neurons. We therefore recommend users to not run destVI with less than 50 spots.

Over the course of our experiments, we found a training mini-batch size of max(dataset_size/10, 128) to perform well in deconvolution. We set the maximum batch size to 128 as we saw decreasing performance with a batch size of 512 for the brain dataset. Most likely it is safe to increase the mini-batch size for big datasets and getting runtime benefits. However, we have most experience from experiments with a batch size of 128 and limit the maximum batch size to this value. If runtime is a big concern, manual increase of this parameter is possible. The version with batchsize 128 was already several times faster than Cell2Location.

DestVI with latent amortization showed superior performance in the setting with optimal mini-batch size in small datasets but performance was inferior for other mini-batch sizes. We continue suggesting both amortization and in the case of the brain dataset both amortization schemes were similar in performance.

Please share any feedback with us via twitter (@YosefLab), through the comment section below or through scverse discourse webpage (https://discourse.scverse.org/).

Acknowledgements#

We acknowledge members of the Yosef Lab. We thank Adam Gayoso for reviewing the changes to destVI and bringing the benchmarking study to our attention.

Bibliography#

(1) Romain Lopez, Baoguo Li, Hadas Keren-Shaul, Pierre Boyeau, Merav Kedmi, David Pilzer, Adam Jelinski, Ido Yofe, Eyal David, Allon Wagner, Can Ergen, Yoseph Addadi, Ofra Golani, Franca Ronchese, Michael I. Jordan, Ido Amit and Nir Yosef. DestVI identifies continuums of cell types in spatial transcriptomics data. Nature Biotechnology. 2022.

(2) Vitalii Kleshchevnikov, Artem Shmatko, Emma Dann, Alexander Aivazidis, Hamish W. King, Tong Li, Rasa Elmentaite, Artem Lomakin, Veronika Kedlian, Adam Gayoso, Mika Sarkin Jain, Jun Sung Park, Lauma Ramona, Elizabeth Tuck, Anna Arutyunyan, Roser Vento-Tormo, Moritz Gerstung, Louisa James, Oliver Stegle and Omer Ali Bayraktar. Cell2location maps fine-grained cell types in spatial transcriptomics. Nature Biotechnology. 2022.

(3) Bin Li, Wen Zhang, Chuang Guo, Hao Xu, Longfei Li, Minghao Fang, Yinlei Hu, Xinye Zhang, Xinfeng Yao, Meifang Tang, Ke Liu, Xuetong Zhao, Jun Lin, Linzhao Cheng, Falai Chen, Tian Xue and Kun Qu. Benchmarking spatial and single-cell transcriptomics integration methods for transcript distribution prediction and cell type deconvolution. Nature Methods. 2022.

Today we officially released scvi-tools version 0.9.0 (changelog). This release marks the culmination of five months of work on the backend of the codebase, which came after three months of work on the frontend. In this short note, we officially introduce scvi-tools as a readily usable codebase that contains many implementations of probabilistic single-cell omics methods, and also features a high-level interface to accelerate the model development process. We start with some historical notes about our previous codebase, which was mostly used for internal developments in the last three years. We then describe the obstacles we found to its external adoption, and the foundational idea behind the new scvi-tools work: a high-level deep probabilistic programming library specialized for single-cell omics data.

While stochastic gradient-based optimization is highly successful for setting weights and other differentiable parameters of a neural network, it is in general useless for setting hyperparameters -- non-differentiable parameters that control the structure of the network (e.g. the number of hidden layers, or the dropout rate) or settings of the optimizer itself (e.g., the learning rate schedule). Yet finding good settings for hyperparameters is essential for good performance for deep methods like scVI. Furthermore, as pointed out by Hu and Greene (2019) selecting hyperparameters is nessary in order to compare different machine learning models, especially if those are substantially sensitive to hyperparameter variations.

Droplet- based single-cell RNA sequencing (scRNA-seq) datasets typically contain at least 90% zero entries. How can we best model these zeros? Recent work focused on modeling zeros with a mixture of count distributions. The first component is meant to reflect whether such an entry can be explained solely by the limited amount of sampling (on average ~5% or less of the molecules in the cell). The second component is generally used to reflect "surprising" zeros caused by measurement bias, transient transcriptional noise (e.g., "bursty" gene with a short mRNA half life), or true longer-term heterogeneity that can not be captured by a similified (low dimensional) representation of the data. Among others, zero-inflated distributions (i.e., zero-inflated negative binomial) have been widely adopted to model gene expression levels (1, 2).